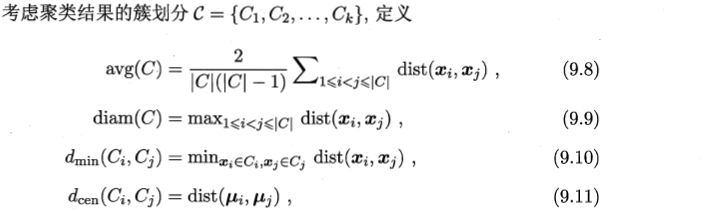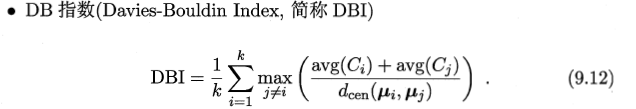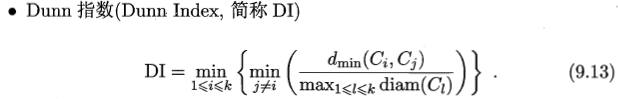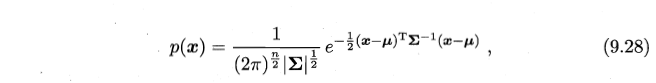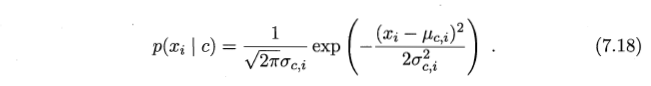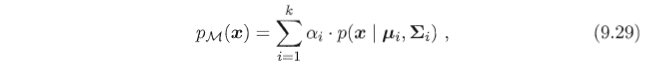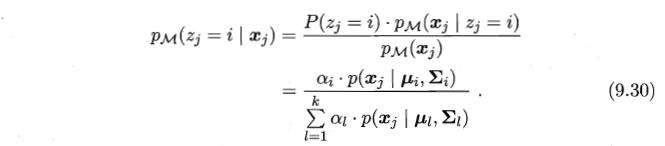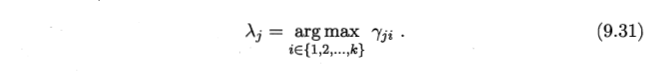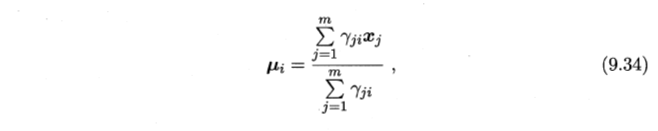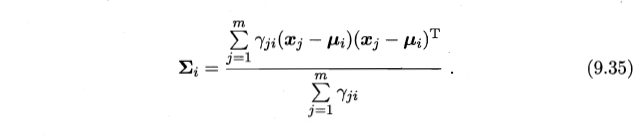聚类
概述
聚类是一种无监督学习方法,它将相似的数据样本分组为一个集合,被称为簇(cluster),使得簇内的样本相似度高,而簇间的样本相似度低。聚类的目标是在不提供先验类别标签的情况下,发现数据中的内在结构和模式。
- **类别:**无监督学习
- **目的:**通过对无标记训练样本的学习来揭示数据的内在性质及规律,为进一步的数据分析提供基础。

性能度量
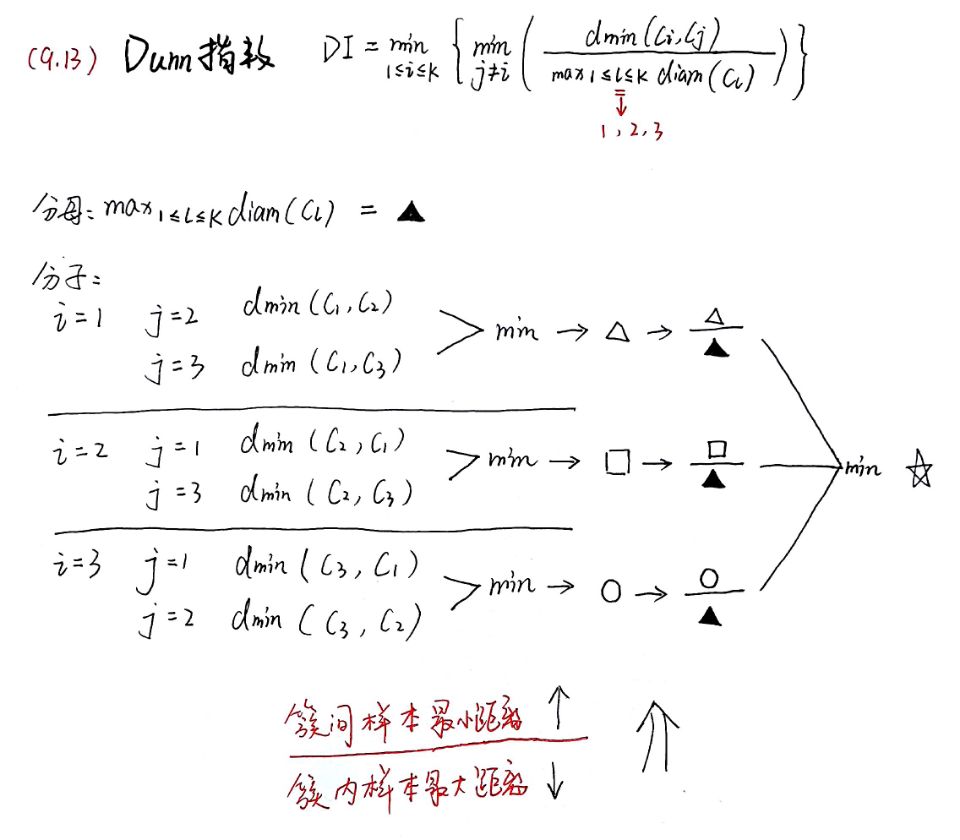
- **结论:**簇内的样本尺度尽可能彼此相似,簇间的样本尽可能不同。
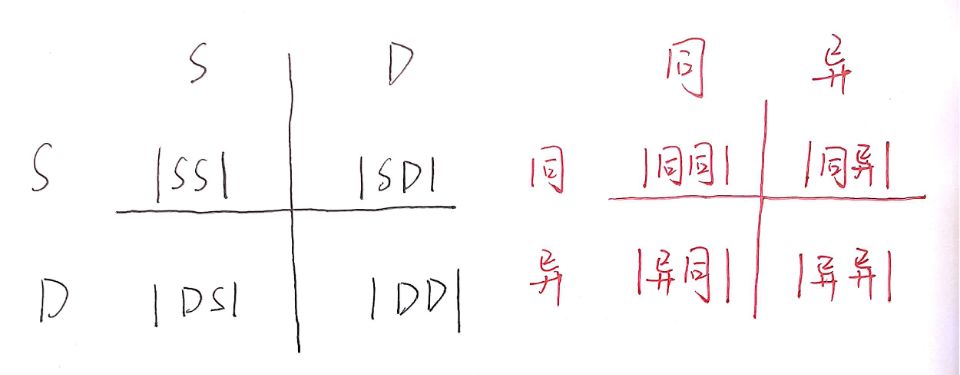
外部指标
-
**外部指标:**将聚类结果与某个 “参考模型” 进行比较,称为 “ 外部指标 ”。





内部指标
-
**内部指标:**直接考察聚类结果而不利用任何参考模型,称为 “ 内部指标 ”。





距离计算
距离度量 / 非距离度量
- 若它是一个 “ 距离度量 ”,则应该满足以下性质:


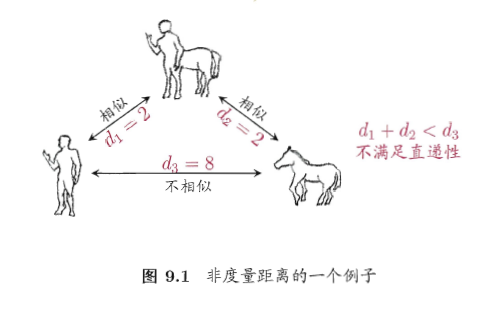
有序属性 / 无序属性
有序属性

- 欧氏距离:
- 曼哈顿距离:
- 切比雪夫距离:

无序属性
混合距离
加权距离
原型聚类
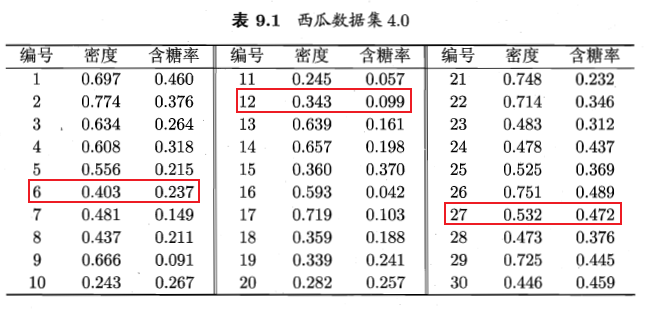
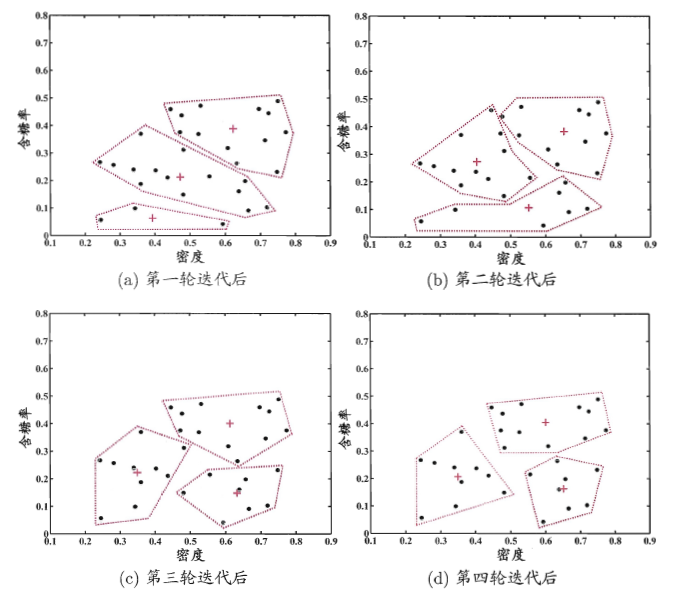
k 均值算法


- 步骤:
- 随机选取样本作为初始均值向量(初始值:k 的值【即几个簇】)
- 分别计算每个样本点到初始均值向量的距离,距离哪个点最近就属于哪个簇
- 每个簇重新计算中心点,重复第二步直到收敛

学习向量量化
和 K-means 的不同:
- 每个样例有类别标签,即 LVQ 是一种监督式学习;
- 输出不是每个簇的划分,而是每个类别的原型向量;
- 每个类别的原型向量不是简单的均值向量,考虑了附近非 / 同样例的影响。


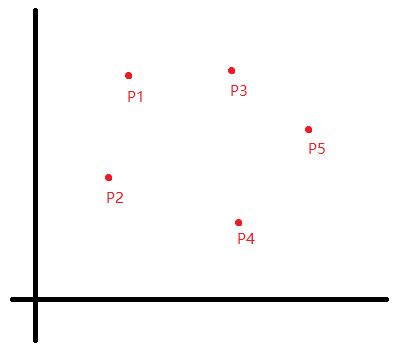
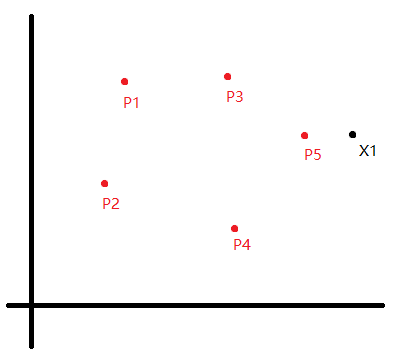
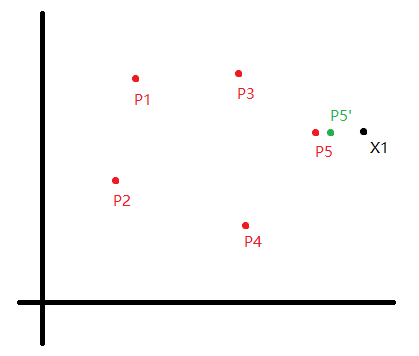
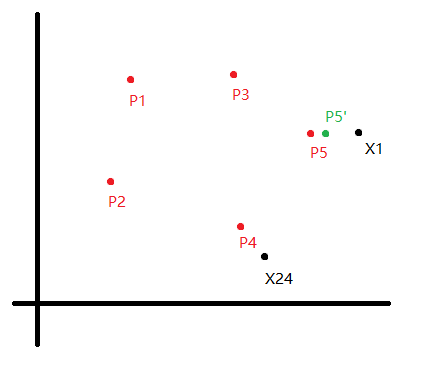

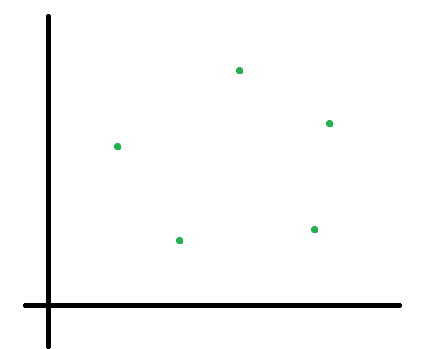
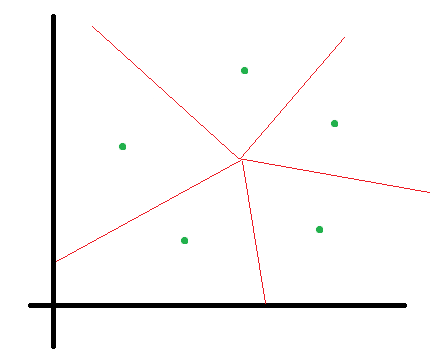

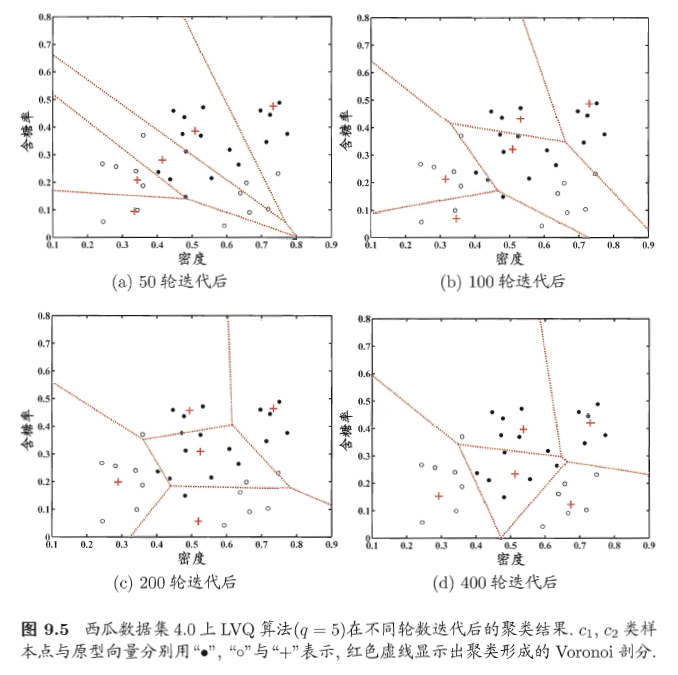
例题:

高斯混合聚类
原先数据集是这个样子的:
某天,被黑客入侵,把两个数据集混合起来了,要怎么分开呢?
首先,我们确定了要分成两个高斯模型,我们随机选取两个 均值 和 方差 作为初始值
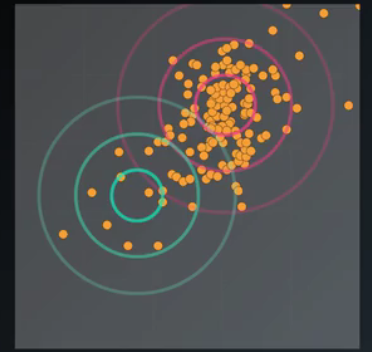
之后,我们分别分析每个点对两个高斯模型的隶属度
做完以后,我们得到越红的点对红色高斯模型的隶属度越高,越绿对绿模型隶属度越高
隶属度又对模型本身的 均值 和 方差 造成影响,于是我们得到了 一次迭代后的 两个高斯模型,可以发现红圈基本没动,绿圈向右上方移动了一点
多次迭代的动画是这样的。

但是通过最开始的数据,我们知道我们的目的是找到下面的两个数据集【黄圈】
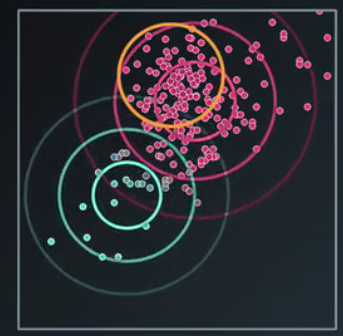

显然我们这次高斯聚类并不成功,这是由于我们给了它不好的初始值【随机值】,所以我们重新做一次,打算来手动输入初始值,那初始值怎么设定呢?我们选择,先用 K 均值的方法,来选定两个中心值,把这两个中心值作为我们的手动输入值,结果变成了这样。

我们发现还是没达到我们想要的效果,因此我们下一步不再使用简单的圆高斯模型,使用协方差矩阵,而不是每个高斯的方差,这样可以使圆圈变成椭圆形
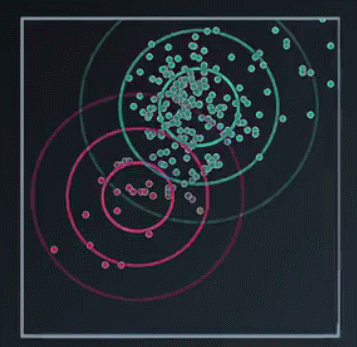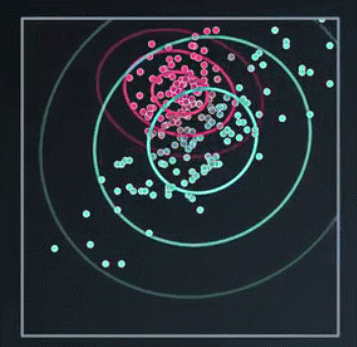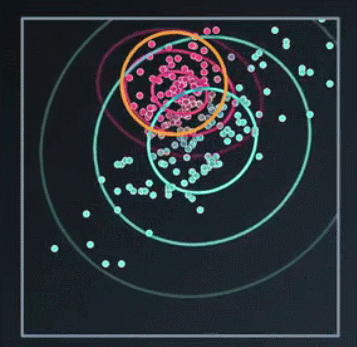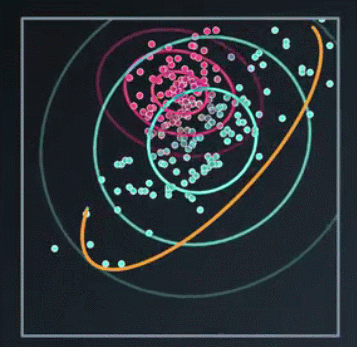
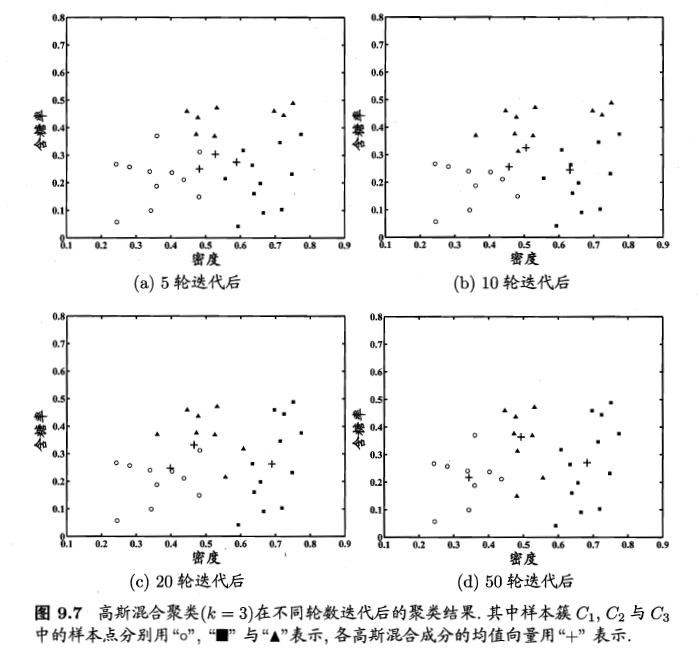
到这里我们只是直观上对高斯模型有个了解,还有一些疑问,比如:图中的圈都带表什么呢?
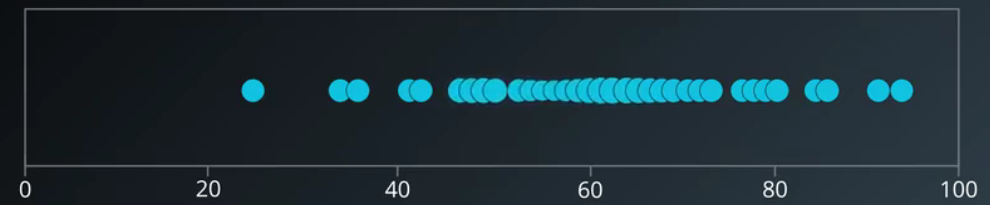
这是一次期中考试的学生成绩分布,很明显他是属于高斯分布(正态分布)的
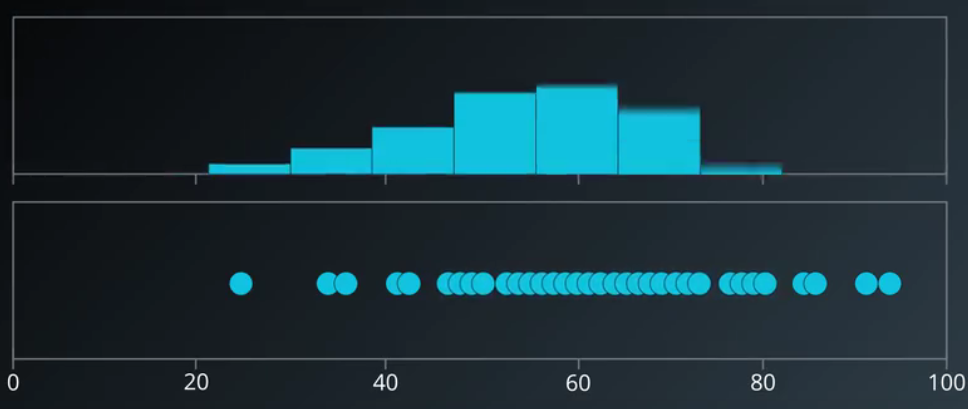
画成柱状图是这样的
经过简单的计算 均值 和 方差 我们能够描绘出他的高斯曲线
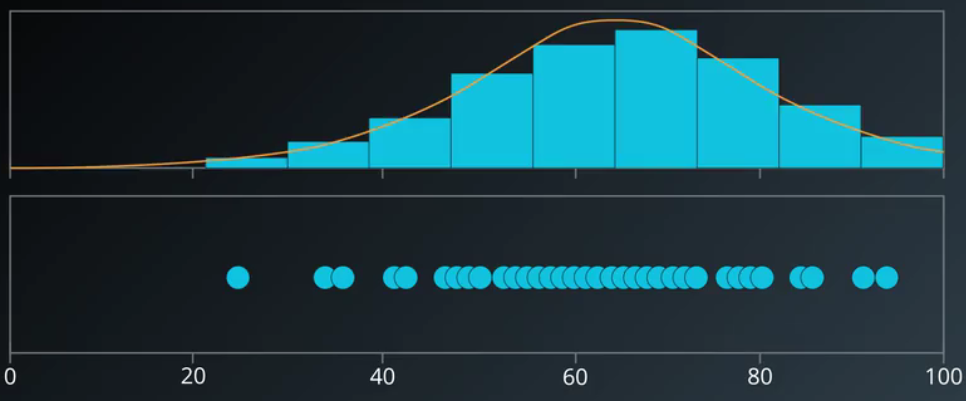
μ 代表平均数,也就是平均成绩
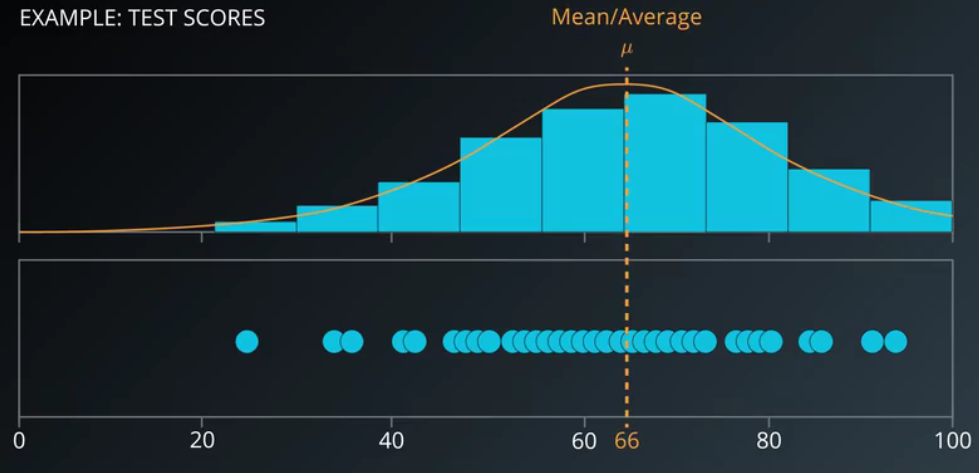
其次是标准差,这个例子中,标准差是15,这很容易计算
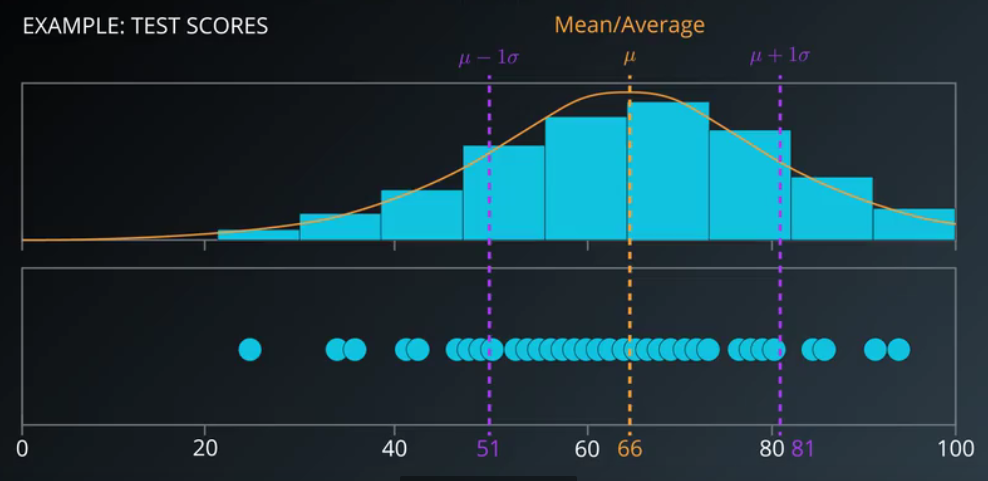
我们发现 【均值 - 1个标准差】 和 【均值 + 1个标准差】,这段区域占总数的 68%,这是高斯分布的属性
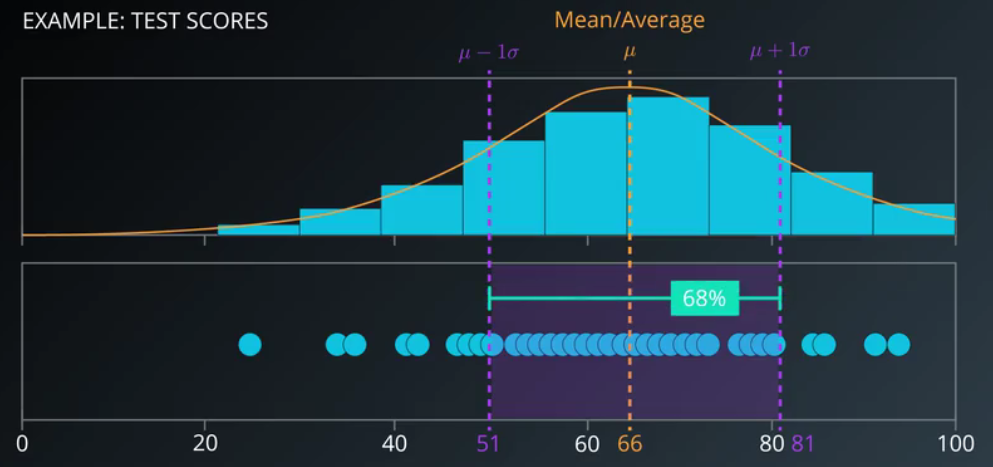
而 【均值 - 2个标准差】 和【 均值 + 2个标准差】,这段区域占总数的 95%

【均值 - 3个标准差】 和【 均值 + 3个标准差】,这段区域占总数的 99%

知道了圈代表什么,还有一个问题,高斯模型我们知道,那高斯混合模型是什么意思呢?
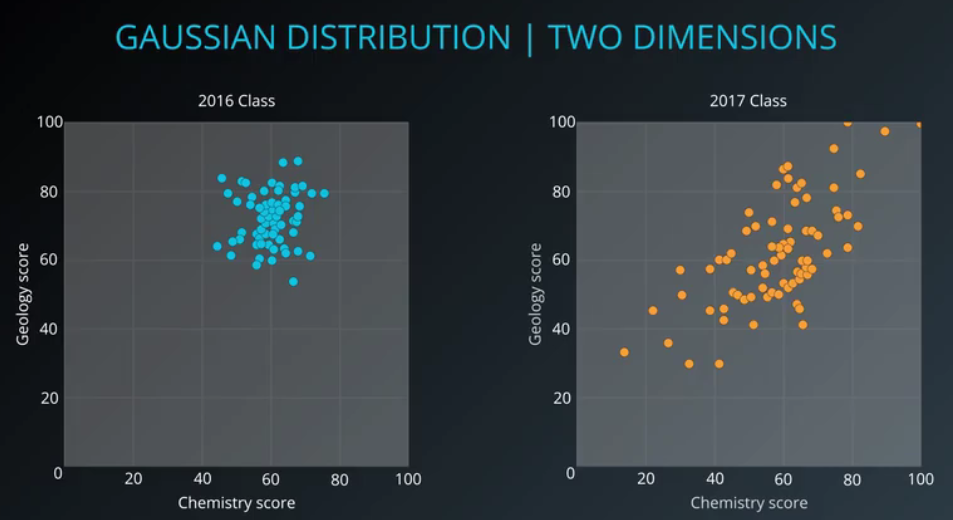
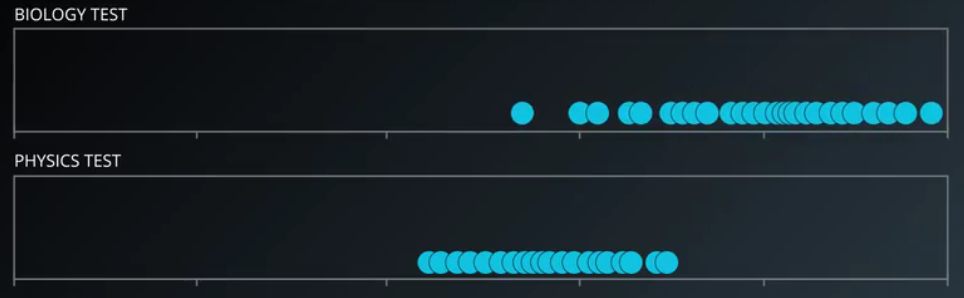
我们看,这里有一个班级的两门课成绩,分别是物理和生物,数轴是以 20 为单位的,我们发现这次生物题比较简单,全班分数都挺高,而物理题比较难,全班成绩都低
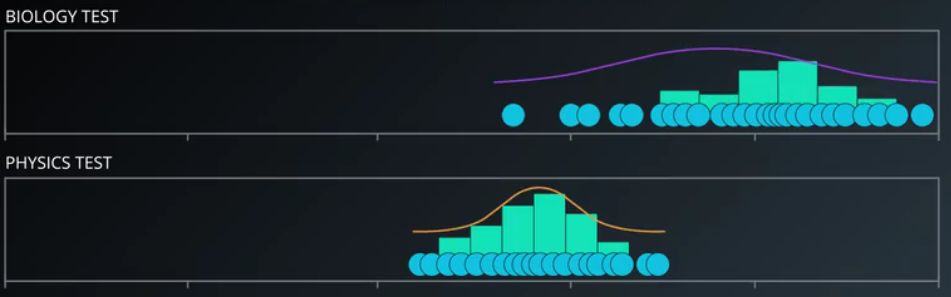
我们把数据绘制成柱状图,通过柱状图我们发现他们都遵循高斯分布,尽管 均值 和 方差 不同,但都是高斯分布
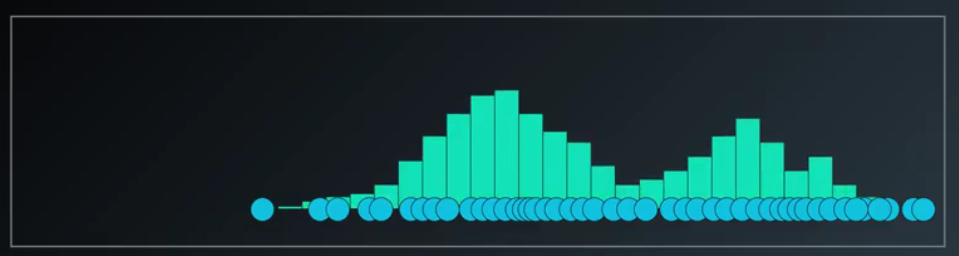
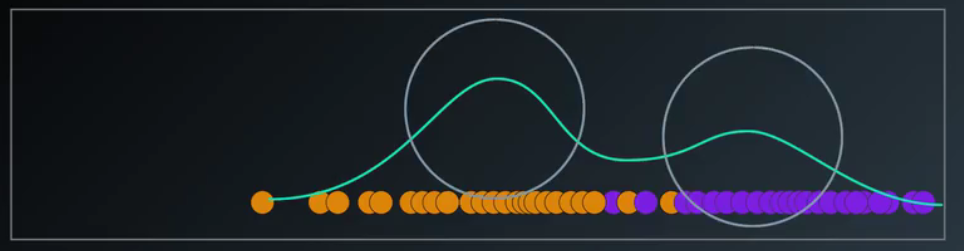
假如就是这个数据集,我们想对它做高斯混合聚类处理,数据叠加到一起是这样的,它是一个模型,但并不是一个高斯分布,它是两个子集和合并,但合并之后并不是高斯分布
它是两个没有标签的高斯分布

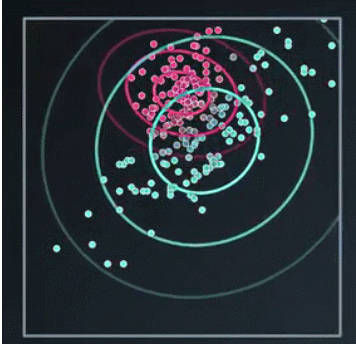
经过计算机的高斯混合聚类,我们得到了这样的结果
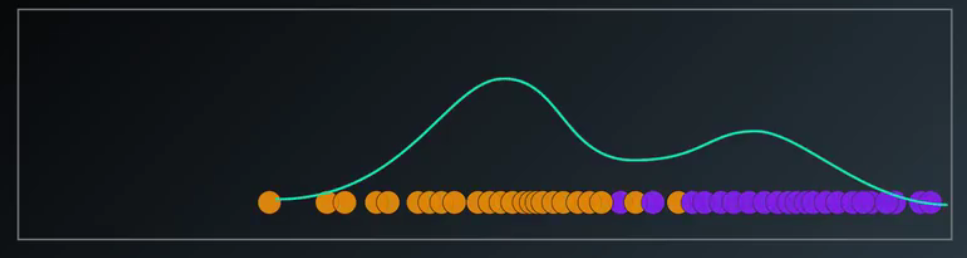
到这里我们知道了,高斯混合分布本身并不是高斯模型,而是两个高斯模型的混合物,哪个点更可能属于哪一个高斯模型,它就被分到哪一个类中,这就是高斯混合模型的最简单的例子。
步骤
- 初始化 高斯混合成分的个数 k ,假设高斯混合分布模型参数 α(高斯混合系数) μ (均值) , Σ(协方差矩阵);
- 分别计算每个样本点的 后验概率 (该样本点属于每一个高斯模型的概率);
- 迭代 α μ , Σ;
- 重复第二步直到收敛。
难点
- 后验概率 (该样本点属于每一个高斯模型的概率)的计算:

- 上述公式由 7.18 相减化简而来

- 上述公式由 7.18 相减化简而来



- 怎样迭代 α μ , Σ;
- α ——通过样本加权平均值来估计
- Σ ——通过样本加权平均值来估计
- μ ——由样本属于该成分的平均后验概率确定
- α ——通过样本加权平均值来估计
例子

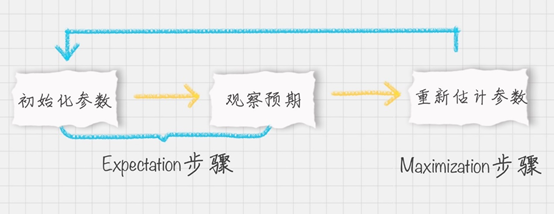
EM思想的体现
密度聚类

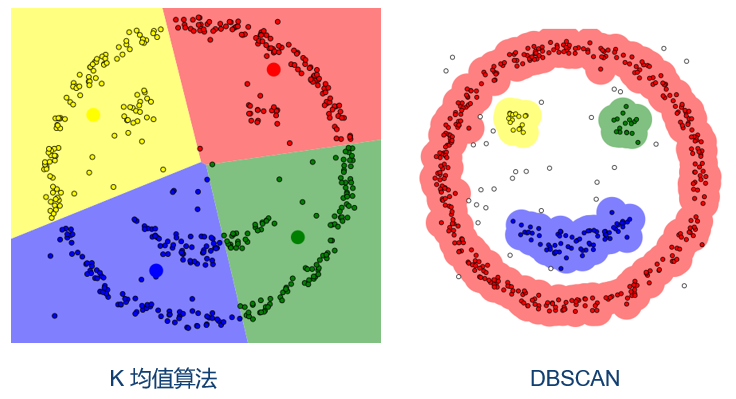
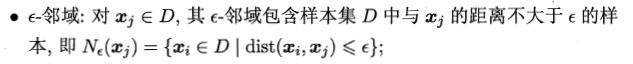

**例题:**初始值:①邻域参数 ε ② 最少点个数 MinPts


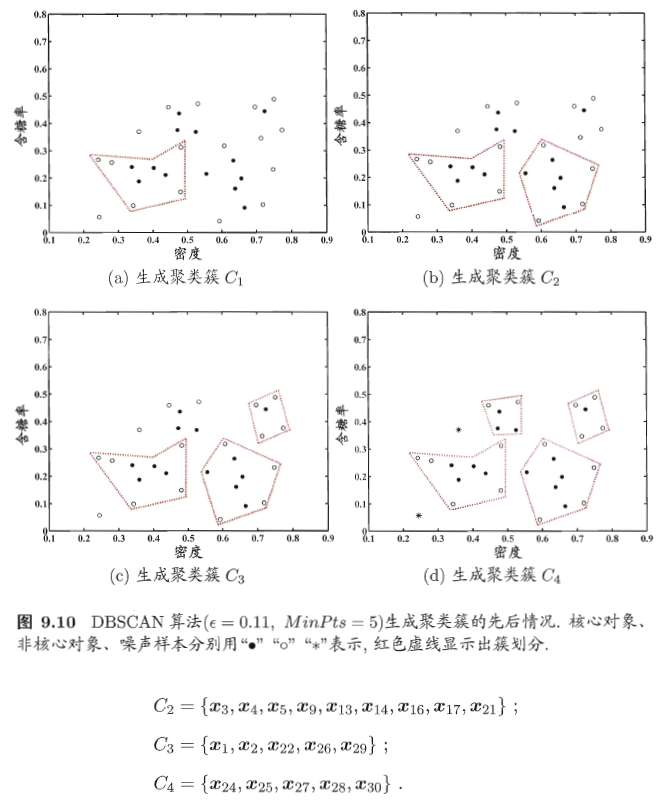
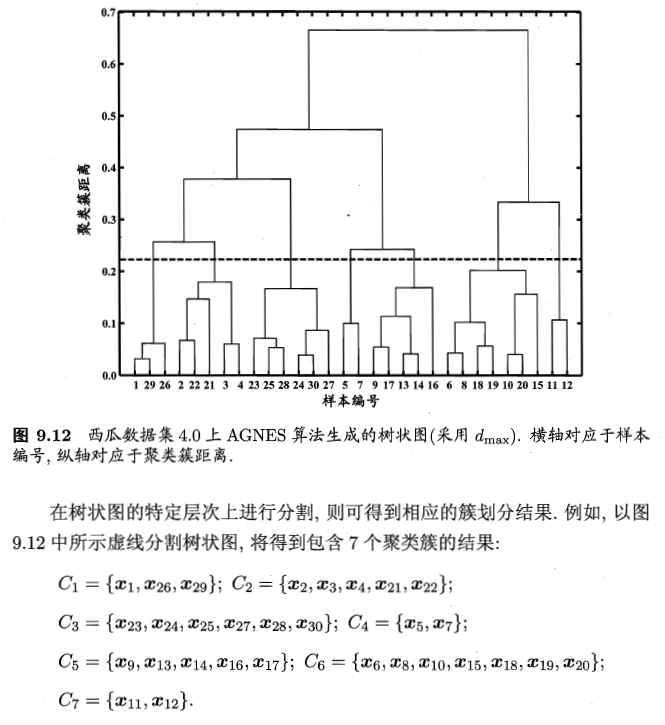
层次聚类

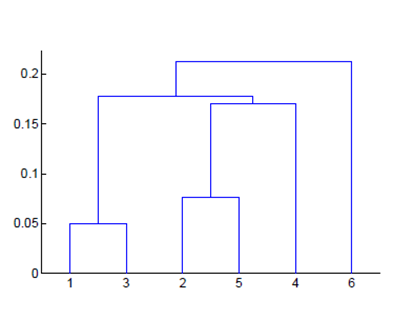
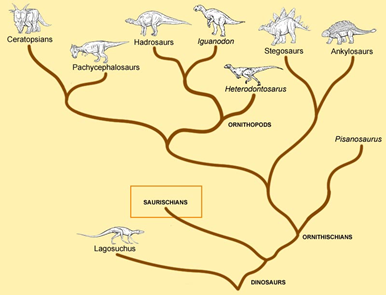

例题: